| Home | Example: FX transactions (US-$/€) |
Example: Weather and radiation |
Example: The 2016 US election and Instagram | Miscellaneous | About Us |
WaveletComp: an R package for computational wavelet analysisWaveletComp is an R package for the continuous wavelet-based analysis of univariate and bivariate time series. Wavelet functions are implemented in WaveletComp such that a wide range of intermediate and final results are easily accessible. The null hypothesis that there is no (joint) periodicity in the series is tested via p-values obtained from simulation, where the model to be simulated can be chosen from a wide variety of options. The reconstruction, and thus filtering, of a given series from its wavelet decomposition, subject to a range of possible constraints, is also possible. WaveletComp provides extended plotting functionality – which objects should be added to a plot (for example, the ridge of wavelet power, contour lines indicating significant periods, arrows indicating the leading/lagging series), which kind and degree of smoothing is desired in wavelet coherence plots, which color palette to use, how to define the layout of the time axis (using POSIXct conventions), and others. Technically, we have developed vector- and matrix-based implementations of algorithms to reduce computation time. Easy and intuitive handling is given high priority in WaveletComp. Keywords: R project; wavelet analysis; Morlet wavelet; (cross-) wavelet power; wavelet coherence; wavelet reconstruction; wavelet graphics; wavelet filtering. A simple example from the WaveletComp guide bookletThe following series was simulated with WaveletComp function periodic.series. Its period is gradually increasing from 20 to 100: The wavelet power spectrum of this series, computed and plotted with WaveletComp functions, is: 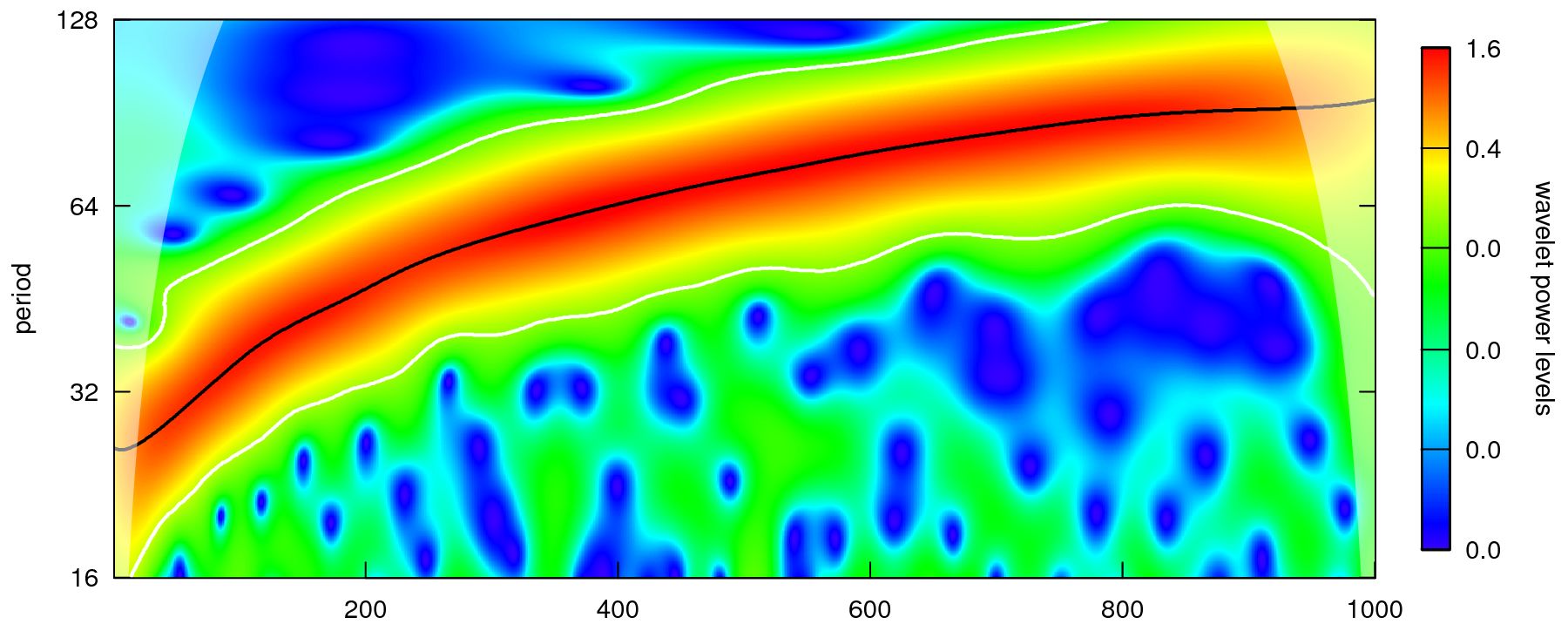 The increasing period is represented by the black line, the ridge of the power spectrum. The period of the time series increases linearly, but the ridge is nonlinear, because periods are powers of 2. The following plot shows a reconstruction of the original series, retaining only significant periods. This is data reduction! One could also call it feature extraction. Only important parts are retained. (What is considered important depends on the application, of course.) |
Verbatim copying and distribution of the material in the entire website of the project WaveletComp are permitted worldwide, without royalty, in any medium, provided this notice, and the copyright notice, are preserved.
